ある自然数に、自然数をかけて自然数の2乗になるようにするという問題を扱ってみたいと思います。
素因数分解をして、次数が偶数でない素数をかければいい、またはペアになっていない素数をかければいいと教わることが多い気がします。
こういう問題がでたらとりあえず、素因数分解をして次数が偶数でない素数をかけたらいい、ペアになっていない素数をかければいいという感じで覚えてしまう子が結構います。
この内容を習いたての頃はこれでも対応できることが多いのですが、時間が経つと何だったかなぁと記憶をたどっても解けないものです。
今回の記事では、自然数をかけてある自然数の2乗、平方数にする方法について書いてみたいと思います。
自然数の2乗の平方数を作るときは素因数分解をするけれど・・・
例題を使って説明していきますね。
まずは小さな数を使ってして解いてみましょう。
12くらいだとなんとなく分かってしまうかもしれませんが、きちんとしたやり方でやってみますね。
まずは12を素因数分解してみましょう。
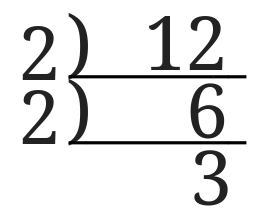
12を素因数分解すると、\(12=2^2\times 3\)となります。
上のような連除法・逆さ割り算・簾算なんて呼ばれる方法でするとやりやすいと思います。
・素因数分解の意味や書き方がわからない!簡単なやり方を解説
\(12=2^2\times 3\)を使って何を掛けると自然数の2乗になるのかについて考えてみます。
次数が偶数でないものやペアになっていない素数を掛ければいいという考え方で考えてみると、2は2乗(ペアになっている)ので、3を掛ければいいとなります。
実際、3を掛けるとある自然数の2乗になるので正解となるのですが、なぜそうするのでしょうか。
なぜ、偶数次数になっていないものを掛けるの?
先ほどの\(12=2^2\times 3\)を変形してみると、$$12=2^2\times 3=(2\times3)\times(2)$$となります。
ある自然数の2乗にするには、\( (ある自然数)\times (ある自然数)\)となれば、ある自然数の2乗になったと言えます。
しかし、\( (2\times3)\times(2)\)の前の括弧と後ろの括弧の数が同じであれば、ある自然数の2乗になるのですが、前の括弧内の3が後ろの括弧内にありません。
つまり、後ろの括弧に3を補うことができれば、\( (2\times3)\times(2\times 3)\)となり、\(6\times 6\)となるので、ある自然数の2乗となることが言えます。
そのためこの場合は、3を掛ければいいということになります。
また、3を掛けることで、6の2乗になることが分かりました。
それでは、もう1題解いてみましょう。
ちょっと数字を大きくしてみました。
まずは60を素因数分解してみましょう。
連除法できちんと書きましょう。
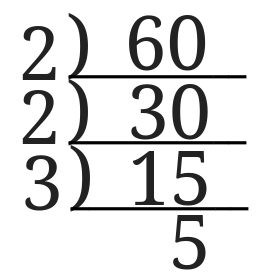
\(60=2^2\times 3\times 5\)となります。
よって、60に\(3\times 5\)、つまり15を掛けると自然数の2乗になることが分かります。
また、どんな自然数の2乗になるのかというと、\(2\times 3\times 5\)、30の2乗になります。
わかりにくいときは、\(60=(2\times 3\times 5)\times(2)\)という感じで考えてみましょう。
前の括弧と後ろの括弧が等しくなれば、何かしらの自然数の2乗になります。
この場合、前の括弧と後ろの括弧を比べてみると、後ろの括弧に\(3\times 5\)が不足しています。
そのため、\(3\times 5\)を掛ければ、ある自然数の2乗にすることができることが分かります。
また、\(3\times 5\)を掛けてみると、\( (2\times 3\times 5)\times(2\times 3\times 5)\)となります。
括弧内を計算すると、\(30\times30\)となり30の2乗になると分かります。
練習問題
小さな自然数を掛けて、ある自然数の2乗になるようにしたい。どんな自然数を掛ければいいですか。また、そのときどんな自然数の2乗になっていますか。
1、24
2、75
3、120
4、210
5、23
解答・解説
1、6を掛けると12の2乗になります。
2、3を掛けると15の2乗になります。
3、30を掛けると60の2乗になります。
4、210を掛けると210の2乗になります。
5、23を掛けると23の2乗になります。
4と5は、ちょっといじわるだったかもしれませんね。
4の210は、素因数分解してみると、\(2\times 3\times 5\times 7\)となるので、全く素数がかぶりません。
そのため、\(2\times 3\times 5\times 7\)をそのまま掛けないと自然数の2乗にすることができないということになります。
5の23は素数なので、23を掛けると23の2乗になります。
まとめ
今回の記事では、自然数をかけてある自然数の2乗、平方数にする方法について書いてみました。
この問題は中間考査や期末考査のような定期考査でもよく出てくる問題です。
きちんと分かっていれば、得点源にしやすい問題のなので、しっかりできるようにしておきましょう。
素因数分解そのものができないという場合はまずは素因数分解をできるようにするといいですね。
素因数分解さえできれば、後は、どんな数を掛けるのかを考えれば答えを出すことができます。




