以前の記事では、2の平方根は分数や小数では書き切れないということについて書いてみました。
分数で書けない数といえば\(\pi\)が登場して以来初めてではないでしょうか。
分数や小数では書き切れないので、2の平方根は±√2と書きましたね。
・平方根のイメージは?√2などの素因数分解では求められない数の場合を使って解説!
実際、数字では書ききれないのですが、線分の長さでは√2や√3などを作図することは可能です。
今回の記事では√2を線分の長さで書いてみたいと思います。
√2の長さを作図で求める
三平方の定理(ピタゴラスの定理)を使ってだと書きやすいと思いますが、中学3年生が平方根を習ったときにはまだ三平方の定理は習っていません。
三平方の定理を使うと中学3年では難しくなるので、三平方の定理を使わずに作図したいと思います。
√2の長さってどのくらい?
√2を作図してもその長さが√2かどうかということはわかりにくいものです。
定規ではかるわけにも行きませんし、そもそも√2の長さがいくらかという近似値を計算で求めてもきっちりとした数値は分かりません。
どれくらいの長さか分からなければ、実際に√2を作図できたのかの確認ができません。
そこで、平方根の定義を使ってうまく√2を長さで表したいと思います。
√2は、2の平方根ですね。
面積が2の正方形を考えたときに、その一辺が√2となるはずです。[1]正方形の面積は一辺×一辺なので、〇の平方根は面積〇の正方形の一辺とみることができます。
つまり面積が2の正方形を書くことができれば、その正方形の一辺の長さが√2にあたるので、√2の長さを作図することができたと言えます。
と、言うことは、面積が2の正方形を作図することを目標に頑張ってみましょう。
√2の作図では正方形を使うと…
面積が2の正方形を書いてみましょう。
シュッと書くことができましたか。
書けたのならなかなか勘が鋭いですね。
面積が2の正方形を書くには方眼紙を使うととても簡単に面積が2の正方形を書くことができます。
ただ、面積が\(1cm^2\)の正方形を二つ並べても長方形にしかならないのでだめです。
あくまで正方形にしないと意味がありません。
ここでちょっと工夫をしてみます。
\(1cm^2\)の正方形に対角線を引いてみましょう。
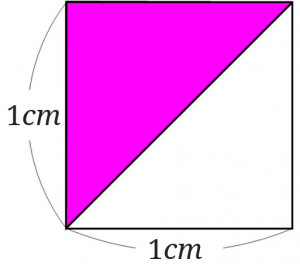
すると、面積が\(1cm^2\)の正方形を2等分することができました。
この対角線を引いた正方形を4つ組み合わせてみるとこんな感じの正方形ができました。
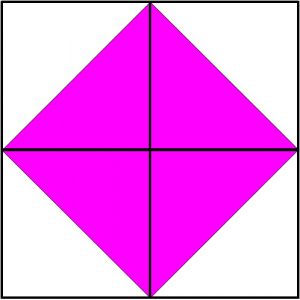
ちょっと正方形が傾いているような感じになっています。
この正方形の面積が\(2cm^2\)になっていますよね。
小さい正方形を半分にしてできた直角二等辺三角形1つの面積は\(0.5cm^2\)です。
この直角二等辺三角形4つからこの正方形はできているので、この正方形の面積は\(2cm^2\)となります。
面積が\(2cm^2\)の正方形を書くことができたので、この正方形の一辺の長さは√2ということになります。
直接√2の長さを書くのは難しいので、面積が\(2cm^2\)の正方形を書くことで√2を作図することができました。
√3の作図は難しい
同じようにして√3の作図は、できなくもないのですが、どうしても三平方の定理を使わないと難しいです。
説明そのものは、三平方の定理を使わなくてもできますが、なぜそのように作図しようと思ったのかを考えると、微妙な感じになってしまいます。
√3の作図は三平方の定理を習ってからで十分だと思います。
√2の作図は直感的にも理解しやすかったのではないでしょうか。
同じように√5も書くことができるので是非チャレンジしてみてくださいね。
まとめ
今回の記事では√2を線分の長さで書いてみました。
三平方の定理を習うと√3の作図もとてもやりやすくなります。
平方根を習ってからしばらくすると根号を使った√2や√3のような数を扱うようになります。
やり方そのものは丸暗記でも対応することが不可能ではありませんが、きちんと理屈が分かっていると√2や√3のような数も扱いやすくなります。
今回の記事では√2の作図を扱いましたがこの作図ができたから、何かできるというようなモノではないと思います。
しかし、この作図を通して、√2ってどんな数なのかということが理解できると、平方根の扱いもうまくなるのではないでしょうか。
平方根の意味をしっかり理解するという意味でも作図で表せるようになれるといいですね。
References
| ↑1 | 正方形の面積は一辺×一辺なので、〇の平方根は面積〇の正方形の一辺とみることができます。 |
|---|




